函数算法

返回：数据库

• 经典 JAVA 算法题册
• 8 大排序算法
• JS 排序算法：冒泡、选择、插入、归并、快速、希尔、堆、计数

幂等函数

什么是幂等?
幂等：F(F(x)) = F(x) 多次运算结果一致
_在我们编程中常见幂等：_-
(1)select 查询天然幂等
(2)delete 删除也是幂等,删除同一个多次效果一样
(3)update 直接更新某个值的,幂等
(4)update 更新累加操作的,非幂等
(5)insert 非幂等操作,每次新增一条

注解@Resubmit、@ResubmitDataAspect、@ResubmitLock可以延时再次提交

核心算法

back

一、算法最最基础

• 1、时间复杂度

• 2、空间复杂度

一般最先接触的就是时间复杂度和空间复杂度的学习了，这两个概念以及如何计算，是必须学的，也是必须最先学的，主要有最大复杂度、平均复杂度等，直接通过博客搜索学习即可。

二、基础数据结构

• 1、线性表

列表（必学）
链表（必学）
跳跃表（知道原理，应用，最后自己实现一遍）
并查集（建议结合刷题学习）
不用说，链表、列表必须，不过重点是链表。

• 2、栈与队列

栈（必学）
队列（必学）
优先队列、堆（必学）
多级反馈队列（原理与应用）
特别是优先队列，再刷题的时候，还是经常用到的，队列与栈，是最基本的数据结构，必学。可以通过博客来学习。相关文章：

3、哈希表（必学） 碰撞解决方法：开放定址法、链地址法、再次哈希法、建立公共溢出区（必学） 布隆过滤器（原理与应用） 4、树 二叉树：各种遍历（递归与非递归）（必学） 哈夫曼树与编码（原理与应用） AVL 树（必学） B 树与 B+ 树（原理与应用） 前缀树（原理与应用） 红黑树（原理与应用） 线段树（原理与应用） 5、数组 树状数组 矩阵（必学） 树状数组其实我也没学过，，，，

三、各种常见算法 1、十大排序算法 简单排序：插入排序、选择排序、冒泡排序（必学） 分治排序：快速排序、归并排序（必学，快速排序还要关注中轴的选取方式） 分配排序：桶排序、基数排序 树状排序：堆排序（必学） 其他：计数排序（必学）、希尔排序 对于十大算法的学习，假如你不大懂的话，那么我还是挺推荐你去看书的，因为看了书，你可能不仅仅知道这个算法怎么写，还能知道他是怎么来的。推荐书籍是《算法第四版》，这本书讲的很详细，而且配了很多图演示，还是挺好懂的。

2、图论算法 图的表示：邻接矩阵和邻接表 遍历算法：深度搜索和广度搜索(必学) 最短路径算法：Floyd，Dijkstra（必学） 最小生成树算法：Prim，Kruskal（必学） 实际常用算法：关键路径、拓扑排序（原理与应用） 二分图匹配：配对、匈牙利算法（原理与应用） 拓展：中心性算法、社区发现算法（原理与应用） 图还是比较难的，不过我觉得图涉及到的挺多算法都是挺实用的，例如最短路径的计算等

3、搜索与回溯算法 贪心算法（必学） 启发式搜索算法：A*寻路算法（了解） 地图着色算法、N 皇后问题、最优加工顺序 旅行商问题 这方便的只是都是一些算法相关的，我觉得如果可以，都学一下。像贪心算法的思想，就必须学的了。建议通过刷题来学习，leetcode 直接专题刷。

4、动态规划 树形 DP：01 背包问题 线性 DP：最长公共子序列、最长公共子串 区间 DP：矩阵最大值（和以及积） 数位 DP：数字游戏 状态压缩 DP：旅行商 我觉得动态规划是最难的一个算法思想了，记得当初第一次接触动态规划的时候，是看 01 背包问题的，看了好久都不大懂，懵懵懂懂，后面懂了基本思想，可是做题下不了手，但是看的懂答案。一气之下，再 leetcdoe 专题连续刷了几十道，才掌握了动态规划的套路，也有了自己的一套模板。不过说实话，动态规划，是考的真他妈多，学习算法、刷题，一定要掌握。这里建议先了解动态规划是什么，之后 leetcode 专题刷，反正就一般上面这几种题型。后面有时间，我也写一下我学到的套路，有点类似于我之前写的递归那样，算是一种经验。也就是我做题时的模板，不过感觉得写七八个小时，，，，，有时间就写。

5、字符匹配算法 正则表达式 模式匹配：KMP、Boyer-Moore 6、流相关算法 最大流：最短增广路、Dinic 算法 最大流最小割：最大收益问题、方格取数问题 最小费用最大流：最小费用路、消遣 总结 对于上面设计到的算法，我都提供了感觉还不错的文章，建议大家收藏，然后可以利用零碎的时间进行阅读，有些人可能会觉得上面的算法太多，说实话，我觉得不多，特别是对于在校生的，上面涉及到的算法可以不用很懂，但至少得了解。至于书籍的话，如果你连基本数据结构都还不懂的，建议看《数据结构与算法》相关书籍，例如《大话数据结构》、《数据结构与算法分析》。如果你有一定的基础，例如知道链表，栈，队列，那么可以看《算法第四版》，不过这本书是用 Java 实现的，不过我觉得你只要学过 C，那么可以看的懂。

算法复杂度速查表

back

• 图例

• 数据结构操作

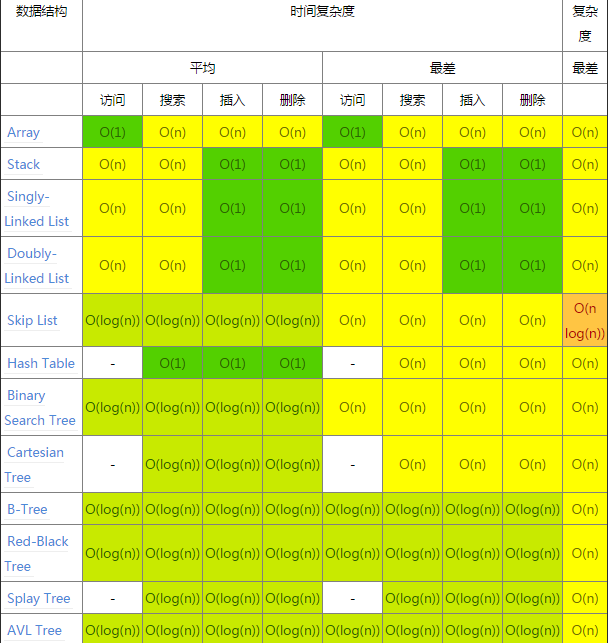
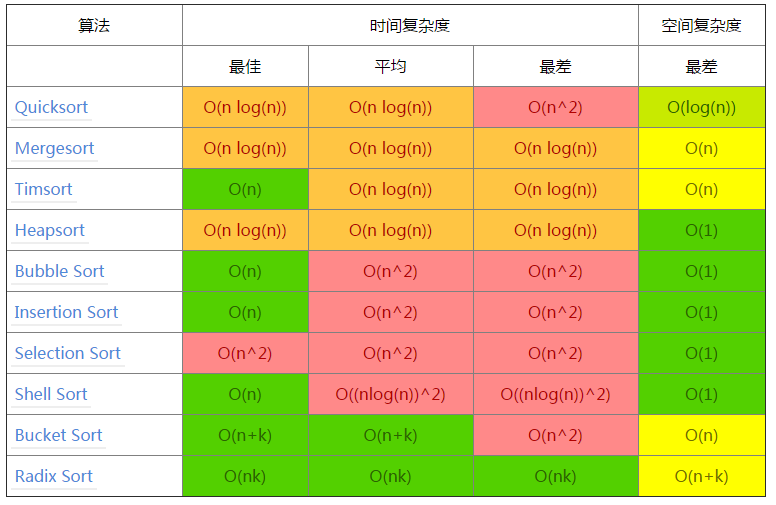
• 数组排序算法

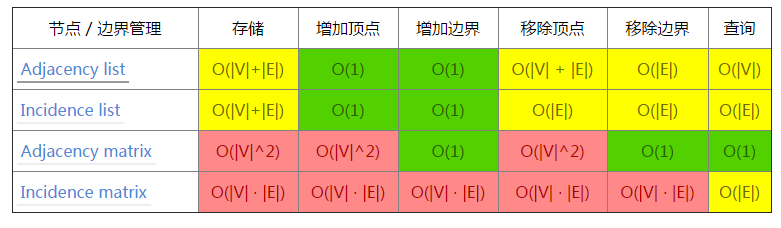
• 图操作

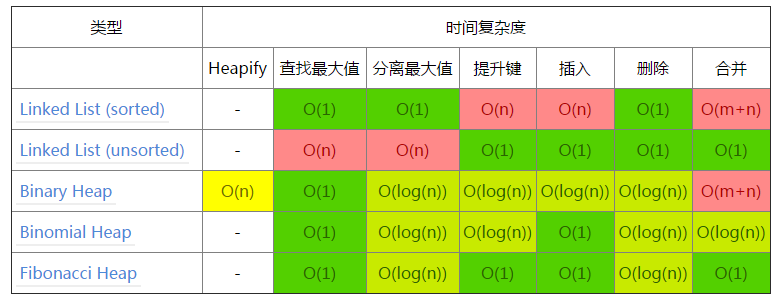
• 堆操作

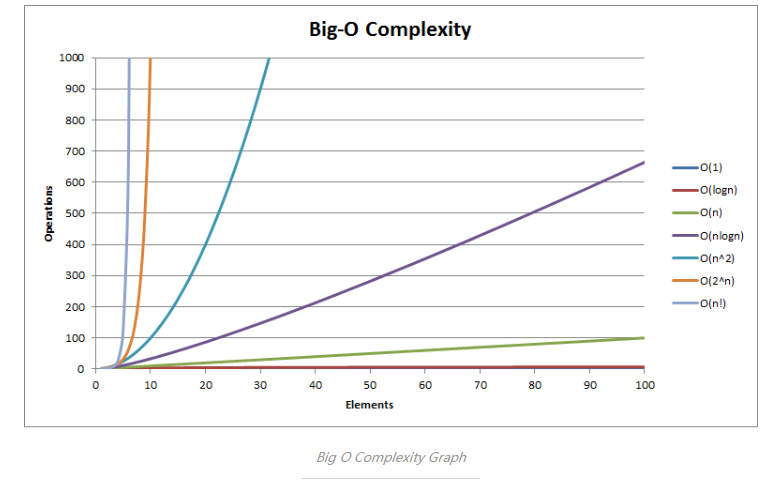
• 大 O 复杂度图表

N 数之和

请用算法实现，从给定的无序、不重复的数组 A 中，取出 N 个数，使其相加和为 M。并给出算法的时间、空间复杂度，

var arr = [1, 4, 7, 11, 9, 8, 10, 6];
var N = 3;
var M = 27;

Result: [7, 11, 9], [11, 10, 6], [9, 8, 10];

我们用 1 和 0 来表示数组中某位元素是否被选中。因此，可以用 0110 来表示数组中第 1 位和第 2 位被选中了。

所以，本题可以解读为：

• 数组中被选中的个数是 N 。
• 被选中的和是 M 。

我们的算法思路逐渐清晰起来：遍历所有二进制，判断选中个数是否为 N ，然后再求对应的元素之和，看其是否为 M 。

从数组中取出 N 个数

如何判断 N=3 是，对应的选取二进制中有几个 1

// 最简单的方式
const n = (num) => num.toString(2).replace(/0/g, "").length;

这里我们尝试使用一下位运算来解决本题，因为位运算是不需要编译的（位运算直接用二进制进行表示，省去了中间过程的各种复杂转换，提高了速度），肯定速度最快。

我们知道 1&0=0 、 1&1=1 ，1111&1110=1110 ，即 15&14=14 ，所以我们每次 & 比自身小 1 的数都会消除一个 1 ，所以这里建立一个迭代，通过统计消除的次数，就能确定最终有几个 1 了

const n = (num) => {
  let count = 0;
  while (num) {
    num &= num - 1;
    count++;
  }
  return count;
};

和为 M

现在最后一层判断就是选取的这些数字和必须等于 M ，即根据 N 生成的对应二进制所在元素上的和 是否为 M

比如 1110 ，我们应该判断 arr[0] + arr[1] + arr[2] 是否为 M。
问题也就转化成了如何判断数组下标是否在 1110 中呢？如在则求和

其实也很简单，比如下标 1 在，而下标 3 不在。我们把 1 转化成 0100 ， 1110 & 0100 为 1100, 大于 0 ，因此下标 1 在。而 1110 & 0001 为 0 ，因此 下标 3 不在。

let arr = [1,2,3,4]
// i 为满足条件的二进制
let i = 0b1110
let s = 0, temp = []
let len = arr.length
for (let j = 0; j < len; j++) {
  if ( i & 1 << (len - 1 - j)) {
 s += arr[j]
 temp.push(arr[j])
  }
}
console.log(temp)
// => [1, 2, 3]

// 参数依次为目标数组、选取元素数目、目标和
const search = (arr, count, sum) => {
  // 计算某选择情况下有几个 1，也就是选择元素的个数
  const getCount = num => {
    let count = 0
    while(num) {
      num &= (num - 1)
      count++
    }
    return count
  }

  let len = arr.length, bit = 1 << len, res = []
  
  // 遍历所有的选择情况
  for(let i = 1; i < bit; i++){
    // 满足选择的元素个数 === count
    if(getCount(i) === count){
      let s = 0, temp = []

      // 每一种满足个数为 N 的选择情况下，继续判断是否满足 和为 M
      for(let j = 0; j < len; j++){
        // 建立映射，找出选择位上的元素
        if(i & 1 << (len - 1 -j)) {
          s += arr[j]
          temp.push(arr[j])
        }
      }

      // 如果这种选择情况满足和为 M
      if(s === sum) {
        res.push(temp)
      }
    }
  }

  return res
}