# 8大排序算法

插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序

# 插入排序

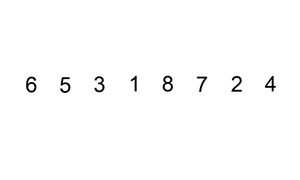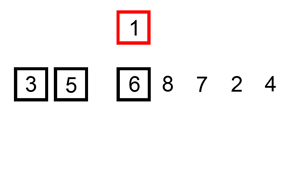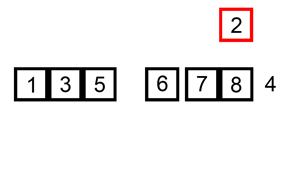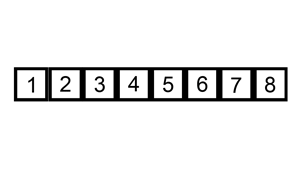
将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置

# 希尔排序

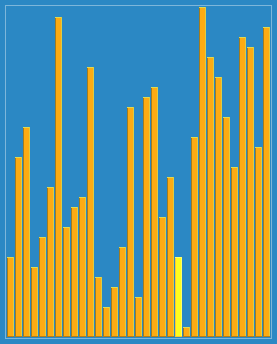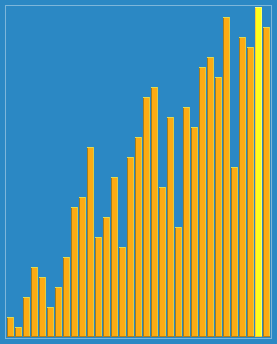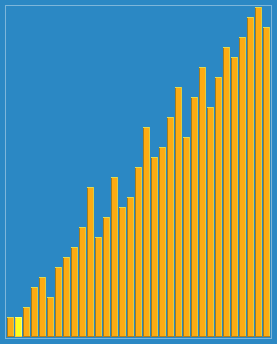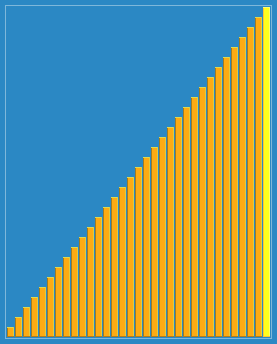
1）选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
2）按增量序列个数k，对序列进行k 趟排序；
3）每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

# 选择排序

1）首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
2）再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
3）重复第二步，直到所有元素均排序完毕。

# 冒泡排序

1）比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2）对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
3）针对所有的元素重复以上的步骤，除了最后一个。
4）持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

# 归并排序

申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
设定两个指针，最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
重复步骤3直到某一指针达到序列尾
将另一序列剩下的所有元素直接复制到合并序列尾

# 快速排序

Ο(n log n)

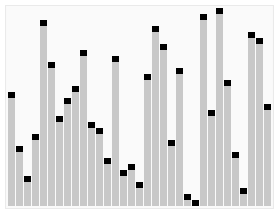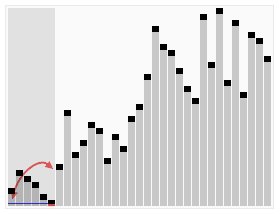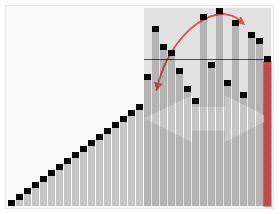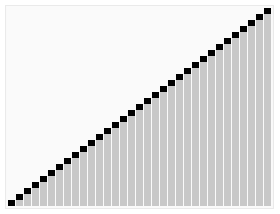
1 从数列中挑出一个元素，称为 “基准”（pivot），
2 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
3 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

# 堆排序

时间复杂度为Ο(nlogn)

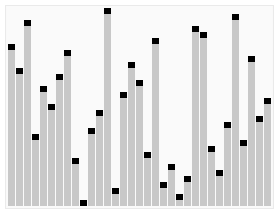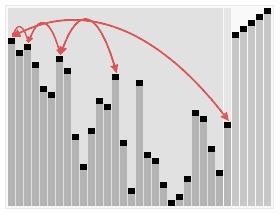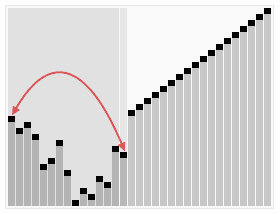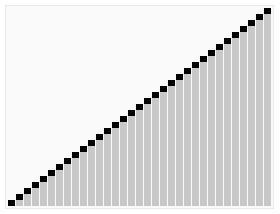
1）创建一个堆H[0..n-1]
2）把堆首（最大值）和堆尾互换
3）把堆的尺寸缩小1，并调用shift_down(0)，目的是把新的数组顶端数据调整到相应位置
4）重复步骤2，直到堆的尺寸为1